Orbital mechanics is a fundamental branch of celestial mechanics and deals with the study of the motion of objects in space under the influence of gravity. The basic principles of om are based on Newton’s and Kepler’s laws of planetary motion. OM focuses on spacecraft trajectories, including orbital manoeuvres consisting of orbital plane changes and interplanetary transfers. A basic understanding of these principles is required to design and control spacecraft to travel to any destination in space or the solar system.
Table of Contents
The standard time system and standard reference frame are the fundamentals necessary for starting with the study of orbital mechanics. It is necessary to evolve the standardization to understand the complex dynamics of the motion of space objects.
This chapter provides an overview of the key concepts and principles of orbital mechanics. It begins with the details of the standards on time and reference frame and then dwells into the important aspects of orbital mechanics.
Standard Time System in Orbital Mechanics
In every branch of science, time is one of the fundamental dimensions. Time is a component of the measuring system used to sequence events, to compare the durations of events and the intervals between them, and to quantify the motion of the object. In astrodynamics or orbital mechanics, time is very critical because objects move fast. To realize a practical time system, we need a precise, repeatable time interval based on some physical phenomenon that we can readily measure and a fundamental epoch from which to count intervals. This leads to the concept of solar time and sidereal time.
Solar Time: Solar time is based on the interval between successive transits of the Sun over a local meridian. Solar time can be further classified into
- Apparent solar time: Time measured concerning the actual position of the Sun.
- Mean Solar Time: Defined to have uniform motion along the celestial equator.
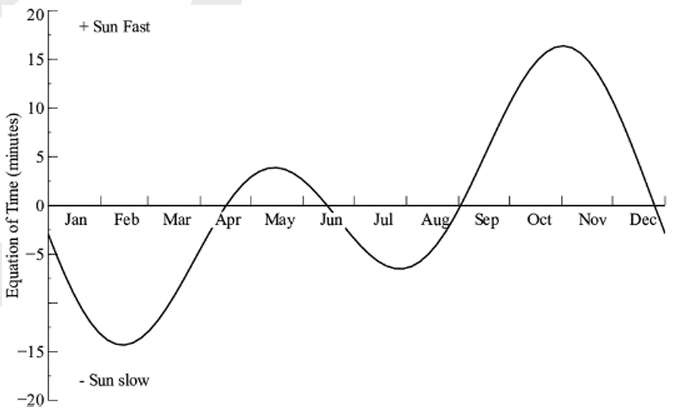
Sidereal time is based on interval between successive transits of a star over a local meridian. Difference between mean time and apparent time is called the equation of time.
Sidereal days are smaller than solar days, 1 Sidereal day = 0.997269566329084 solar days.
- Mean Solar Day (d) = 24 SI hours =86400 SI seconds
- Solar (Tropical) year: 365.242190402d
- Mean Sidereal Day = 23h 56m 4.054s Sidereal Year: 365.256363004d
Since the sun’s apparent motion in right ascension is not uniform, time interval between successive passages of the Sun over a meridian is not constant due to
- Inclination of the Earth’s axis
- The eccentricity of the Earth’s orbit
Atomic Time (TAI) in OM
Atomic time , also known as International Atomic time (TAI) is a highly accurate time system which is independent of the rotation of the Earth, therefore; Atomic Time is a natural system for integrating a spacecraft’s equations of motion. TAI is defined in terms of the oscillations of the caesium atom at mean sea level. The duration of the SI second is defined to be 9,192,631,770 oscillations of the caesium nuclide 133Ce.
TAI was synchronized with Universal Time at the beginning of 1958, and the two have drifted apart ever since, due to the changing motion of the Earth. TAI was exactly 34 seconds ahead of UTC: an initial difference of 10 seconds at the start of 1972, plus 24 leap seconds in UTC since 1972; the last leap second was added on 31 December 2008.
Universal Time: UTC and UT1
All of the universal time (UT) scales are based on the Earth’s rotation with respect to a fixed point (sidereal time) or with respect to the Sun (solar time). The observed universal time (UTO) is determined from observations of stellar transits to determine mean local sidereal time. UT1 is UTO corrected for the Earth’s polar motion and is used when the instantaneous orientation of the Earth is needed. UTC is the basis for all civil time standards. It is also known as Greenwich Mean Time (GMT). The UTC time unit is defined to be an SI second, but UTC is kept within 0.9 seconds of UT1 by occasional leap second adjustments. The equation relating UTC and UT1 is
UT1=UTC+AUT1
Leap Seconds are generally introduced as the last second of any UTC month. December and June months are preferred, March and September are the second choice.
UTC and Time Zone
Local Time is the UTC offset time such that Sun reaches at maximum altitude at local noon. It depends on the local meridian by the relation
LOCAL TIME UTC Time + (Longitude*4) minutes
- To avoid confusion, the world is divided into time zones, each zone corresponding to a whole number of hours before or after UT. This time is known as local time of that meridian.
- A time zone is a region on Earth that has a uniform standard time for legal, commercial, and social purposes.
- Earth is divided into 24 time zones of 15 deg longitude each. Indian Standard time (IST) is defined as follows (Standard meridian of India = 82.5 degree)
IST UTC+ (82.5 *4=330) minutes
Relativistic Time Scales
Between 1976 and 2000, the IAU adopted new relativistic time scales consistent with the general theory of relativity whose unit is the SI second. Note that relativistic times are theoretical (Time not kept on a clock).
Terrestrial Time (TT)
Modern astronomical time standard defined by the IAU, primarily for time-measurements of astronomical observations made from the surface of the Earth. TT is independent of equation of motion theories and uses SI seconds as fundamental interval
TT TAI + 32.184s
Geocentric Coordinate Time (TCG)
A coordinate time having its spatial origin at the center of Earth’s mass.
TCGTT+ LG (JDTT-EJD) 86400
Barycentric Coordinate Time (TCB)
A coordinate time having its spatial origin at the solar system barycenter
TCB-TTL (JD-2443144.5)86400 seconds
In summary, we have the following relations
- UT1 UTC+AUT1
- TAI=UTC+ AAT (leap second correction)
- TTTAI+32.184s
- TCGTT+L (JDTT-EJD) 86400
- TCB TT+L (JDTT-ED) 86400
E.g. epoch: May 14,1990 10:43 UTC is same as:
(1) May 14,1990 10:43:0.04694 UT1
(2) May 14,1990 10:43:57.184 TT
(3) May 14,1990 10:43:57.185 TCB
(4) May 14,1990 10:43:25.000 ΤΑΙ
(5) May 14,1990 10:43:57.478 TCG
Value of AAT = 25s and AUT1 = 0.04694s for May 14,1990 provided by IERS (International Earth Rotation and Reference Systems Service)
Continuous Day/Time: Julian day
Julian day number is a count of days elapsed since Greenwich mean noon on 1 January 4713 В.С., Julian’s proleptic calendar.
- It is the Julian day number followed by the fraction of the day elapsed since the preceding noon
- This is convenient for astronomers as it avoids the date skip during night observation.
- This format is convenient for easy calculation of elapsed days between two events
Standard Reference Frames
In general, motion of a satellite is usually defined in terms of its position and velocity vectors as functions of time. Hence a reference frame/coordinate frames is required with respect to which the position and velocity vectors are defined.
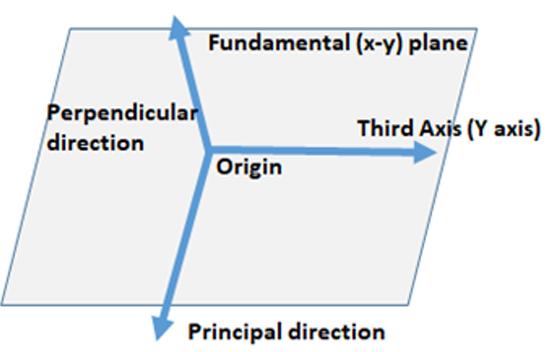
There are five steps in specifying a coordinate system
- Pick the origin.
- Pick the fundamental plane.
- Pick a perpendicular to it.
- Pick the principal direction.
- Add the third axis using the Right-Hand Rule (RHR).
Reference Frames and Types
When the origin and reference plane are kept fixed in space and the reference axis pointed towards distant stars, then the reference frame is fixed in space. Inertial reference frames are the reference frames which are either fixed in space or are moving with uniform velocity, without rotation with respect to distant stars.
Inertial frames
- Inertial frames are non-accelerating frames.
- Newton’s law’s of motion hold in Inertial frames.
- Perfectly Inertial reference frames do not exist in reality.
e.g. EME2000/12000 reference Frame (Pseudo Inertial reference frames)
Non-Inertial frames
- Rotating frames rotate with respect to Inertial frames, the directions of axes are not constant w.r.t. inertial frames
- Centers may accelerate
e.g. ECEF Reference frame, Topocentric, Dynamical frames
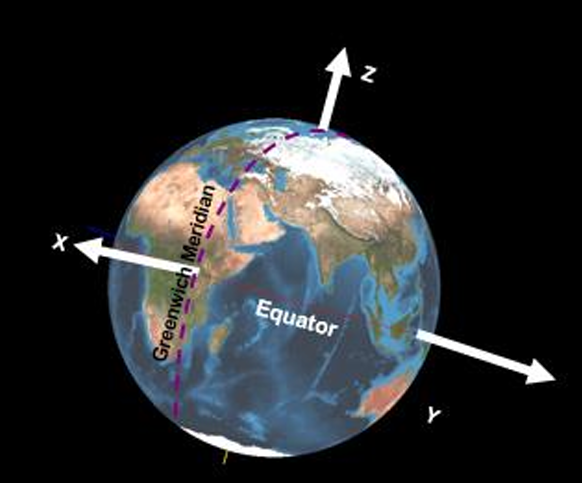
EME2000/12000 Reference Frame
The Earth Mean Equator and Equinox of epoch 12000 (EME2000) inertial reference (which is also known as 12000) is defined using the mean equinox at epoch J2000. J2000 is defined as 1 Jan 2000 at 12:00:00.00 TDB, which corresponds to JD 2451545.0 TDB. The EME2000 reference system is a right-handed Cartesian set of three orthogonal axes (see Figure 3-4) defined as follows:
- +ZEME2000 is normal to the Earth mean equator at epoch J2000
- +XEM 2000 is parallel to the vernal equinox of the Earth mean orbit at J2000
- YEME2000 completes the right-handed system. This coordinate frame need not be centered at the Earth.
ECEF Reference Frame
The Earth Centered Earth Fixed Reference (ECEF) frame is defined as follows:
- The z-axis is defined as being parallel to the earth rotational axes, pointing towards north.
- The x-axis intersects the sphere of the earth at the 0° latitude, 0° longitude.
- The y-axis is perpendicular to both x and z
and forms a right-handed triad. ECEF rotates with the Earth around its z-axis at an angular velocity of approximately 15°/hour (360° over 24 hour). Therefore, coordinates of a point fixed on the surface of the Earth do not change in this frame.
Realization of Inertial Frames
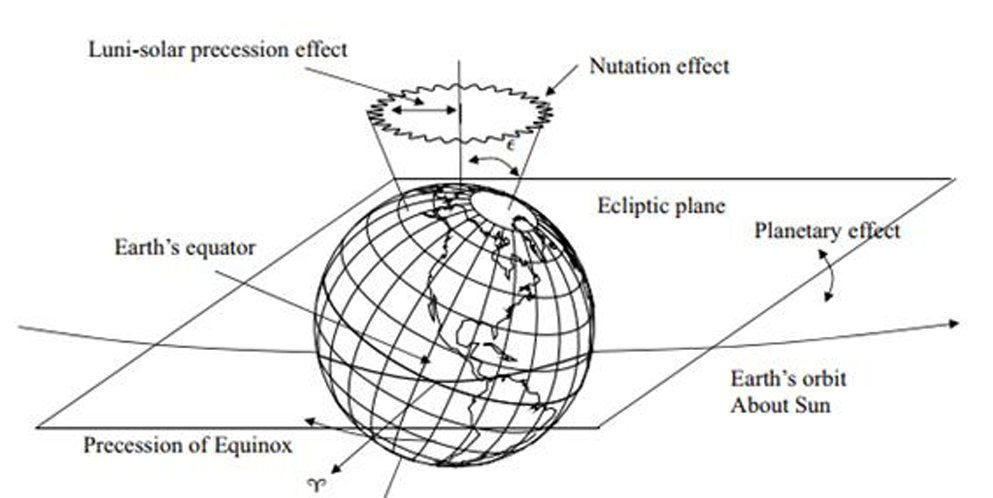
For particular application, most analysis use a reference frame which is sufficiently inertial. Heliocentric reference frame can be considered inertial while dealing with the orbits of planets around the Sun. The motion of objects orbiting the Earth needs an inertial frame for description. To get an inertial frame centered at Earth, the observation from Earth fixed axis must account the following irregularities:
- Long term Irregular motion around its polar axis (Precession)
- Short term irregular motion around its polar axis (Nutation)
- Slightly irregular rotation rate of earth around its axis (Sidereal rotation).
- Very slow pole motion of Earth
The accuracy of the inertial frame realization is dependent on the accuracy of the models for these irregularities ie. precession, nutation, sidereal rotation and polar motion. Once we account for these models in our transformation from Earth Centered Earth Fixed frame (ECEF) we realize a pseudo inertial reference frame called as J2000 or EME2000 (Earth Mean Equator and Equinox of J2000
Precession
It refers to the movement of the rotational axis of a body, such as a planet, with respect to inertial space. The spin axis of the Earth traces out a conical shape in a cycle of approximately 25,765 years, because of the gravitational forces of the Sun and the Moon, and to a lesser extent other bodies, on the equatorial bulge of the spinning Earth.
Nutation
It is a slight irregular motion in the axis of rotation of a largely axially symmetric object, such as a gyroscope or a planet. It happens due to the tidal forces which cause the precession of the equinoxes vary over time so that the speed of precession is not constant.
Sidereal Rotation
The Sidereal rotation coordinate measures the angle through which the Earth has turned in a given period. The angular difference between the direction of the 0° meridian on the Earth and the direction to a point defined in space astronomically is called as sidereal angle or sidereal time. It gives the accumulated precession and nutation in right ascension. The calculations are given below
Polar Motion
The angles (x_{p_{0}} y), which characterize the direction of the rotational pole within the Earth and are the measure of the position of the Earth’s instantaneous pole of rotation in an inertial reference frame:
- Xp coordinate is measured along the 0° (Greenwich) meridian.
- y, the coordinate is measured along the 90 W meridian.
These two coordinates determine the directions on a plane onto which the polar motion is projected. The rotation matrix is given by:
[P]=ROT2(-x_{p})ROT1(-y_{p})
Reference Frame Transformations
Finally, transformation from Inertial (r_{f2000},v_{f2000}) to Non-Inertial reference system (TECEF, VECEF) is done by accounting precession, nutation, sidereal rotation and polar motion. This procedure is well known as FK5 Reduction.
ECEF-Earth Centred Earth Fixed Frame (Rotation reference frame)
12000= [PREC] x [NUT] × [ST] × [PM] X T(ECER)
VJ2000 = [PREC] x [NUT] × [ST] × {[PM] X VECEF + omega (r) × TECEF)
Where,
- omega_{r}= Earth rotation rate
- PREC = Precession Matrix
- NUT = Nutation Matrix
- ST= Sidereal Rotation Matrix
- PM = Polar Motion Matrix
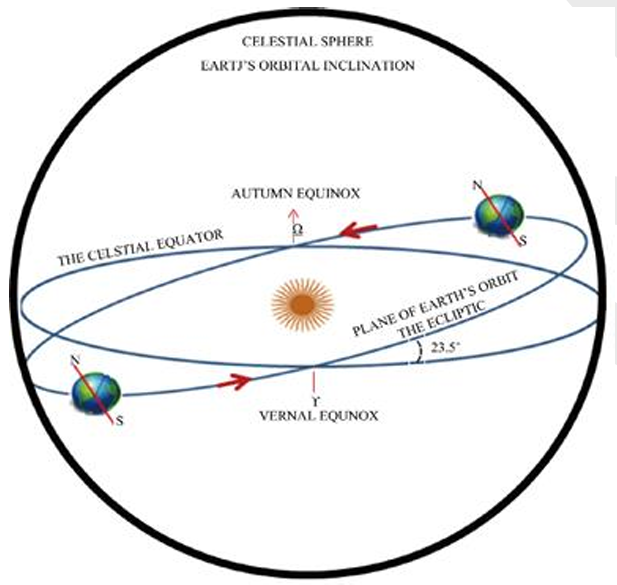
Vernal Equinox: Reference Direction in Space
This defines a fixed vector in space through the center of the Earth to a known celestial coordinate point. The Vernal Equinox drifts at a rate of ~0.014°/ year. Orbits are therefore calculated for a specified date and time, (most often Jan 1, 2000, 2050 or today). It defines as a fixed vector in space through the center of the Earth to a known celestial coordinate point

